아빠가 들려 주는 [통계] Regression과 ANCOVA의 만남(2)

아빠가 들려 주는 [통계] Regression과  ANCOVA의 만남(2)

오늘은 "Regression과  ANCOVA의 만남" 두번째 시간입니다.

지난 번에는 그냥 ANCOVA가 뭔가, 왜 그런 것을 도입하고,

옛날 선배들은 왜 그것을 필요로 했었고,

어떤 방식으로 해결했나를 살펴 보겠습니다.

사실 오늘이 진짜 이야기 입니다.

Regression과  ANCOVA의 만나는 이야기 이니까요.

먼저 Regression하기 좋도록 왼쪽표처럼 바꿉니다. 

ANCOVA에 썼던 자료가 오른쪽 표죠.같은 내용입니다.

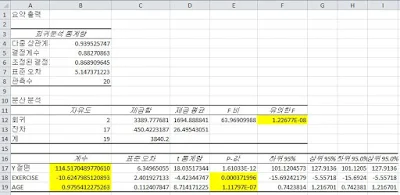
역시 엑셀 자체에서 제공하는 Regression의 결과입니다.

중요하게 볼만한 것을 노란색으로 표시했습니다.

사실 다른 것도 중요하지만........

계수를 이용해서, 이렇게 아래와 같은 회귀식을 만들 수 있습니다.

Y값은 혈압이고,

이것은 excercise와 age에 의해서 표현됩니다.

그런데 excercise는0과 1로만 되어 있고, age는 연속변수이죠.

저 위쪽 표를 보면 알 수 있습니다. 

이렇게, excercise는 0과 1을 각각 넣어 보겠습니다.

단 age는 연속변수니까 평규값인 51.55를 넣어 보겠습니다.

아래 표는 지난번에 ANOVA 했을 때 보았던 그 표입니다.

기억나시죠?

잘 보면 adjusted means이 위의 회귀식에서 구해진 값과 일치합니다.

뭔가 느낌이 오시나요?

즉 adjusted means은 바로 회귀식에서 구해지는 값입니다.

지난번에 ANCOVA 할 때도 삼각형을 그려서

age를 보정하기 위해 평균으로 끌어왔던 것이 기억나시죠?

동영상으로 보여 주었던거......

바로 그 작업을 회귀분석에서는 쉽게 해 버리는 것입니다.   

그리고, 아래의 표는 ANCOVA에서의 p값입니다.

그런데, 이 p값은 저기.. 위 쪽의 회귀분석에서 Excercise의 p값과 같습니다.

----------------------------------------------------------------------

자 이렇게 보면 분명해 집니다.

ANCOVA는 ANOVA 처럼 Excercise의관점에서접근합니다.

age는 하나의 교란변수로 취급하는 셈이지요.

regression은 Excercise나 age 모두 하나씩의 변수로 접근합니다.

그렇지만, 결론은 같습니다.

그리고, regression이 어쩌면 더 폭넓고,

포함하는 것이라고 볼 수도 있습니다.

ANOVA는 기본적으로 처리할 수 있는 교란변수가 한개, 많아야 두개로 제한됩니다.

regression은 제한이 없죠.

(사실 이게 문제이긴 합니다... 그 이야기는 다음에....)